Rank selection diagnostics with graphical output

nmfkc.rank provides diagnostic criteria for selecting the rank (\(Q\)) in NMF with kernel covariates. Several model selection measures are computed (e.g., R-squared, silhouette, CPCC, ARI), and results can be visualized in a plot.

By default (save.time = FALSE), this function also computes the Element-wise Cross-Validation error (Wold's CV Sigma) using nmfkc.ecv.

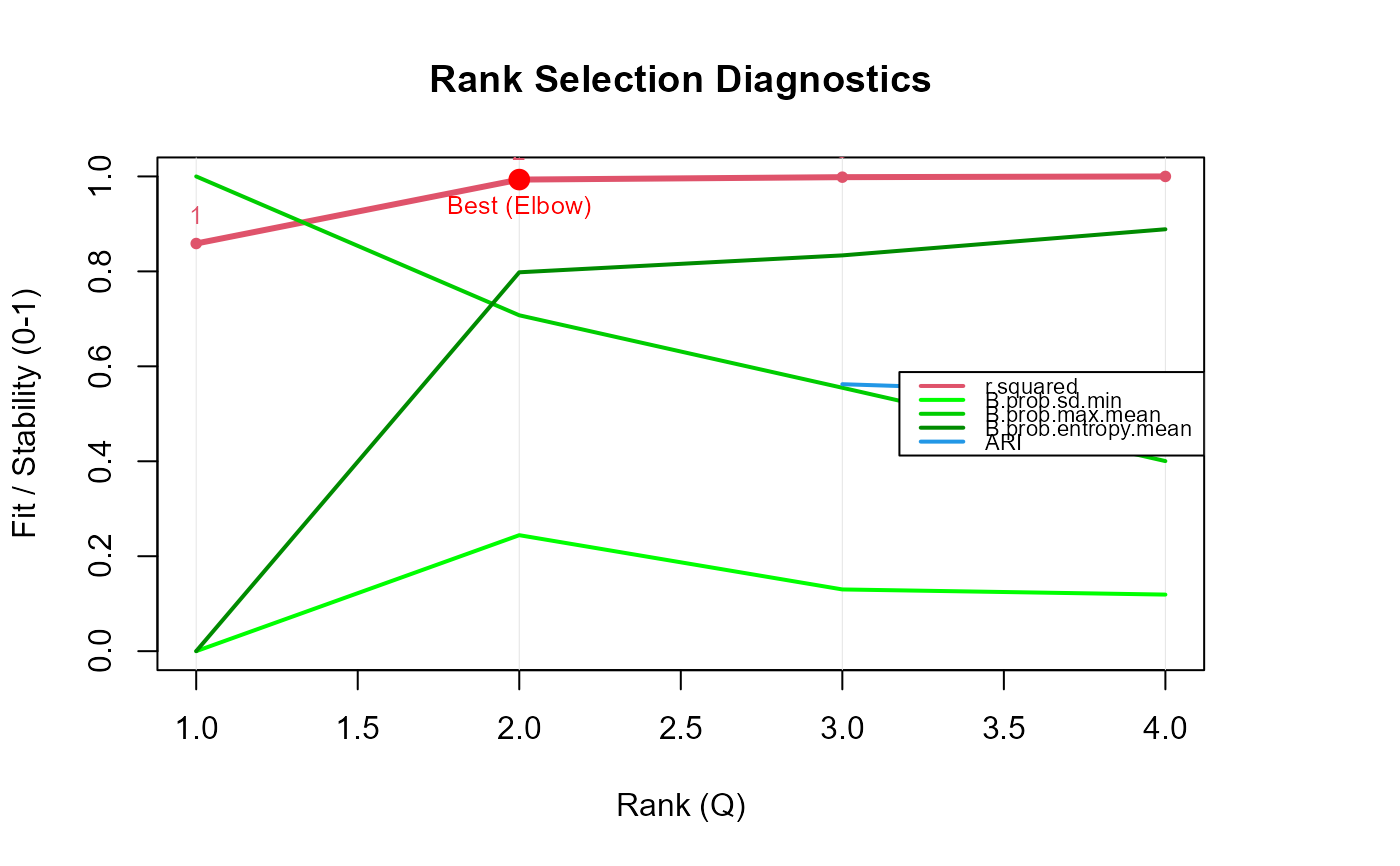
The plot explicitly marks the "BEST" rank based on two criteria:

Elbow Method (Red): Based on the curvature of the R-squared values (always computed if Q > 2).
Min RMSE (Blue): Based on the minimum Element-wise CV Sigma (only if save.time=FALSE).

nmfkc.rank(Y, A = NULL, rank = 1:2, save.time = FALSE, plot = TRUE, ...)

Arguments

Y

Observation matrix.

A

Covariate matrix. If NULL, the identity matrix is used.

rank

A vector of candidate ranks to be evaluated.

save.time

Logical. If TRUE, skips heavy computations like Element-wise CV. Default is FALSE (computes everything).

plot

Logical. If TRUE (default), draws a plot of the diagnostic criteria.

...

Additional arguments passed to nmfkc and nmfkc.ecv.

Q: (Deprecated) Alias for rank.

Value

A list containing:

rank.best: The estimated optimal rank. Prioritizes ECV minimum if available, otherwise R-squared Elbow.
criteria: A data frame containing diagnostic metrics for each rank.

References

Brunet, J.P., Tamayo, P., Golub, T.R., Mesirov, J.P. (2004). Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA, 101, 4164–4169. doi:10.1073/pnas.0308531101 Punera, K., & Ghosh, J. (2008). Consensus-based ensembles of soft clusterings. Applied Artificial Intelligence, 22(7–8), 780–810. doi:10.1080/08839510802170546

Examples

# install.packages("remotes")
# remotes::install_github("ksatohds/nmfkc")
# Example.
library(nmfkc)
Y <- t(iris[,-5])
# Full run (default)
nmfkc.rank(Y, rank=1:4)
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec
#> Running Element-wise CV (this may take time)...
#> Performing Element-wise CV for Q = 1,2,3,4 (5-fold)...
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec

#> $rank.best
#> [1] 4
#> 
#> $criteria
#>   rank r.squared      ICp         AIC        BIC B.prob.sd.min
#> 1    1 0.8586795  52.4309   -50.91409   621.8162     0.0000000
#> 2    2 0.9933479 102.3992 -1579.36199  -233.9015     0.2443194
#> 3    3 0.9984511 153.9677 -2147.71982  -129.5291     0.1300233
#> 4    4 0.9999888 202.0625 -4800.29737 -2109.3764     0.1191841
#>   B.prob.entropy.mean B.prob.max.mean       ARI silhouette      CPCC  dist.cor
#> 1           0.0000000       1.0000000        NA         NA        NA 0.9410181
#> 2           0.7980677       0.7075007        NA  0.8692814 0.9264254 0.9746472
#> 3           0.8336790       0.5548794 0.5623250  0.5358708 0.9193853 0.9489567
#> 4           0.8887089       0.4003933 0.5404919  0.3049893 0.8966046 0.9464434
#>   sigma.ecv
#> 1 1.1694153
#> 2 0.7997277
#> 3 0.7786008
#> 4 0.7674663
#> 
# Fast run (skip ECV)
nmfkc.rank(Y, rank=1:4, save.time=TRUE)
#> Y(4,150)~X(4,1)B(1,150)...
#> 0sec
#> Y(4,150)~X(4,2)B(2,150)...
#> 0sec
#> Y(4,150)~X(4,3)B(3,150)...
#> 0sec
#> Y(4,150)~X(4,4)B(4,150)...
#> 0sec

#> $rank.best
#> [1] 2
#> 
#> $criteria
#>   rank r.squared      ICp         AIC        BIC B.prob.sd.min
#> 1    1 0.8586795  52.4309   -50.91409   621.8162     0.0000000
#> 2    2 0.9933479 102.3992 -1579.36199  -233.9015     0.2443194
#> 3    3 0.9984511 153.9677 -2147.71982  -129.5291     0.1300233
#> 4    4 0.9999888 202.0625 -4800.29737 -2109.3764     0.1191841
#>   B.prob.entropy.mean B.prob.max.mean       ARI silhouette CPCC dist.cor
#> 1           0.0000000       1.0000000        NA         NA   NA       NA
#> 2           0.7980677       0.7075007        NA         NA   NA       NA
#> 3           0.8336790       0.5548794 0.5623250         NA   NA       NA
#> 4           0.8887089       0.4003933 0.5404919         NA   NA       NA
#>   sigma.ecv
#> 1        NA
#> 2        NA
#> 3        NA
#> 4        NA
#>

Rank selection diagnostics with graphical output

Arguments

Value

References

See also

Examples