NMF-SEM with nmfkc • nmfkc

Overview

This vignette demonstrates how to fit the NMF-SEM (Nonnegative Matrix Factorization–Structural Equation Model) implemented in the nmfkc package.

NMF-SEM extends standard nonnegative matrix factorization by introducing a structural equation model in latent space.

Observed endogenous variables $Y_1$ are approximated as

$Y_1 \approx X (\Theta_1 Y_1 + \Theta_2 Y_2).$

If the feedback operator $XC_1$ is stable, the model implies the equilibrium mapping

$\hat Y_1 \approx (I - X\Theta_1)^{-1} X\Theta_2 Y_2 \equiv M_{\mathrm{model}} Y_2.$

1. Load and preprocess data

library(lavaan)
#> Warning: package 'lavaan' was built under R version 4.4.2
#> This is lavaan 0.6-19
#> lavaan is FREE software! Please report any bugs.
data(HolzingerSwineford1939)

d <- HolzingerSwineford1939
index <- complete.cases(d)
d <- d[index, ]

1.1 Construct exogenous variables

d$age.rev <- -(d$ageyr + d$agemo / 12)
d$sex.2 <- ifelse(d$sex == 2, 1, 0)
d$school.GW <- ifelse(d$school == "Grant-White", 1, 0)
d[, c("id", "sex", "ageyr", "agemo", "school", "grade")] <- NULL

1.2 Nonnegative normalization

library(nmfkc)
#> Package: nmfkc (Version 0.5.8 , released on 20 12 2025 )
#> https://ksatohds.github.io/nmfkc/
d <- nmfkc::nmfkc.normalize(d)

2. Split into endogenous and exogenous blocks

exogenous_vars <- c("age.rev", "sex.2", "school.GW")
endogenous_vars <- setdiff(colnames(d), exogenous_vars)

Y1 <- t(d[, endogenous_vars])
Y2 <- t(d[, exogenous_vars])

3. Baseline NMF model

myepsilon <- 1e-6
Q0 <- 3

res0 <- nmfkc(
  Y = Y1,
  A = Y2,
  Q = Q0,
  epsilon = myepsilon,
  X.L2.ortho = 100
)
#> Y(9,300)~X(9,3)C(3,3)A(3,300)=XB(3,300)...0.1sec

M.simple <- res0$X %*% res0$C

3.5 Hyperparameter Tuning for Sparsity (Optional)

grid_params <- expand.grid(
    C1.L1     = c(0,1:9/10,1:10),
    C2.L1     = c(0,1:9/10,1:10)
)
n_iter <- nrow(grid_params)
mae.cv <- 0*1:n_iter

for(i in 1:n_iter){
  if (i %% round(n_iter / 10) == 0) {
    message(sprintf("Processing... %d%% (%d/%d)", round(i/n_iter*100), i, n_iter)) 
  }  
  p <- grid_params[i, ]
  res.cv <- nmf.sem.cv(Y1, Y2, rank = Q0,
                       X.init = res0$X,
                       X.L2.ortho = 100,
                       C1.L1 = p$C1.L1,
                       C2.L1 = p$C2.L1,
                       seed = 1, epsilon = myepsilon)
  mae.cv[i] <- res.cv
}

f <- data.frame(grid_params,mae.cv)
f <- f[order(f$mae.cv),]
head(f,5)
#    C2.L2.off C1.L1 C2.L1    mae.cv
#140         0    10   0.6 0.1820841
#160         0    10   0.7 0.1820843
#180         0    10   0.8 0.1820877
#200         0    10   0.9 0.1820907
#120         0    10   0.5 0.1820908
print(p <- f[1,])

4. NMF-SEM estimation

p <- list(C1.L1 = 10, C2.L1 = 0.6)

res <- nmf.sem(
  Y1, Y2,
  rank = Q0,
  X.init = res0$X,
  X.L2.ortho = 100,
  C1.L1 = p$C1.L1,
  C2.L1 = p$C2.L1,
  epsilon = myepsilon
)

plot(res$objfunc.full, type = "l",
     main = "Objective Function",
     ylab = "Loss", xlab = "Iteration")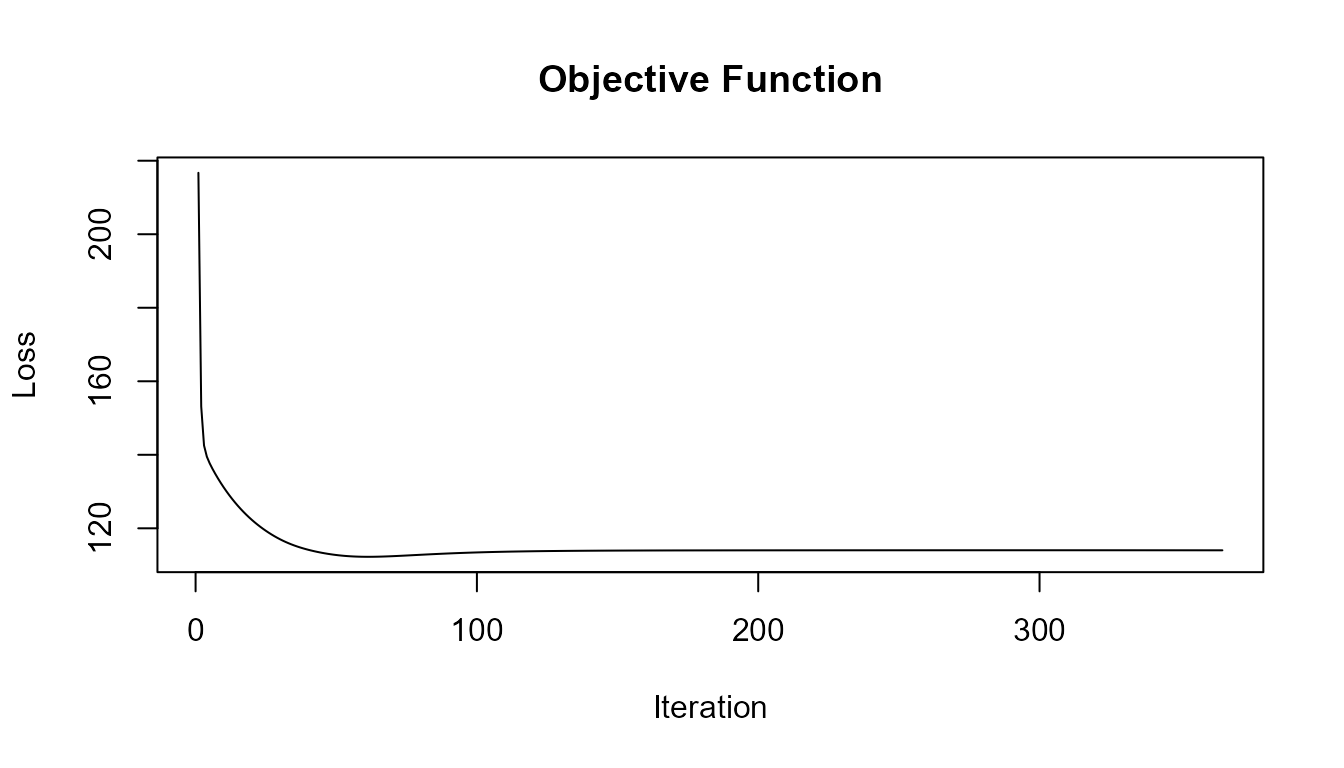

5. Diagnostics

SC.map <- cor(as.vector(res$M.model),
              as.vector(M.simple))

cat("Q=     ", Q0, "\n")
#> Q=      3
cat("RHO=   ", round(res$XC1.radius, 3), "\n")
#> RHO=    0.35
cat("AR=    ", round(res$amplification, 3), "\n")
#> AR=     1.358
cat("SCmap= ", round(SC.map, 3), "\n")
#> SCmap=  0.999
cat("SCcov= ", round(res$SC.cov, 3), "\n")
#> SCcov=  0.98
cat("MAE=   ", round(res$MAE, 3), "\n")
#> MAE=    0.181

6. Visualization

res.dot <- nmf.sem.DOT(
  res,
  weight_scale = 5,
  rankdir = "TB",
  threshold = 0.01,
  fill = FALSE,
  cluster.box = "none"
)

library(DiagrammeR)
#> Warning: package 'DiagrammeR' was built under R version 4.4.3
grViz(res.dot)